Phân phối mẫu

Trong phần này, ta dùng phần mềm R (một ngôn ngữ lập trình trong thống kê) để mô phỏng phân phối mẫu của trung bình và phân phối mẫu của phương sai, phân phối mẫu cho tỷ lệ sẽ được trình bày bên dưới sau ví dụ mô phỏng cho phân phối mẫu của trung bình và phương sai.

Giả sử là một mẫu ngẫu nhiên được lấy từ tổng thể có phân phối chuẩn với trung bình và phương sai .Khi đó và

Ví dụ minh họa cho bằng hình ảnh

Lưu ý là biến ngẫu nhiên trung bình của mẫu và là mẫu ngẫu nhiên bao gồm các giá trị trung bình kích thước n

Ý tưởng: Lấy mẫu kích thước 100 từ phân phối chuẩn N(8,4) và tính giá trị trung bình mẫu. Lặp lại quá trình trên 1000 lần để được mẫu . Khi đó nếu thì đồ thị histogram của mẫu sẽ có hình dáng giống với đồ thị của hàm mật độ phân phối chuẩn N(0,1)

Bước 1: Lấy mẫu kích thước 100 từ phân phối chuẩn với trung bình 8 và độ lệch chuẩn là 2 sau đó tính trung bình ta được giá trị của biến ngẫu nhiên

> X=function(){
+ mean(rnorm(100,8,2))}
> X()
[1] 8.127551

Bước 2: Lặp lại việc lấy mẫu như vậy 1000 lần ta được giá trị mẫu của

> MauX=replicate(1000,X())

> MauX

[1] 8.177542 7.630873 7.779065 7.893846 7.882159 7.598194 7.872815 8.453036
[9] 7.792972 8.046070 8.030402 8.194805 7.939913 7.771466 8.127705 7.689597
[17] 7.802307 8.314282 7.947374 7.839685 7.924071 8.453053 8.206735 8.179007
[25] 7.668324 8.141854 8.010416 7.995762 8.135584 8.197215 8.144798 8.330804
[33] 8.004587 7.946060 8.052466 7.730231 8.220357 8.168854 7.816897 8.346156

...

[985] 7.988645 8.317452 8.319720 8.212151 7.522727 7.949834 7.378931 8.225489
[993] 8.396495 7.912937 7.727440 8.070288 7.930439 7.776631 8.079226 8.054889

Bước 3: Thành lập mẫu của ngẫu nhiên

> Y=(MauX-8)/(2/sqrt(100))
> Y

[1] 0.8877120446 -1.8456356074 -1.1046754953 -0.5307695036 -0.5892067736
[6] -2.0090287850 -0.6359257223 2.2651783493 -1.0351396302 0.2303494583
[11] 0.1520120493 0.9740270121 -0.3004349565 -1.1426707667 0.6385251941

...

[991] -3.1053435368 1.1274429115 1.9824741682 -0.4353136362 -1.3627991670
[996] 0.3514386149 -0.3478056503 -1.1168473937 0.3961305389 0.2744453988

Bước 4: Vẽ đồ thị histogram tần suất mẫu của mẫu trên với số khoảng chia là 40 và so sánh với phân phối chuẩn N(0,1)

> hist(Y,breaks=40,freq=FALSE)
> curve(dnorm(x),add=TRUE,col="BLUE")

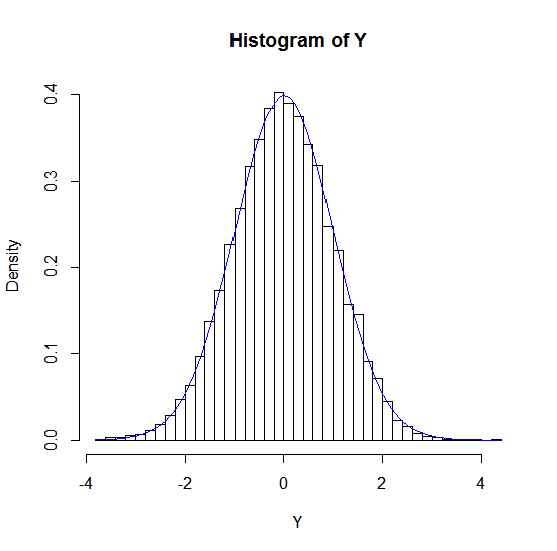
Ví dụ minh họa cho bằng hình ảnh

Ý tưởng: Lấy mẫu kích thước 100 từ phân phối chuẩn N(8,4) và tính giá trị phương sai mẫu. Lặp lại quá trình trên 1000 lần để được mẫu . Khi đó nếu thì đồ thị histogram của mẫu sẽ có hình dáng giống với đồ thị của hàm mật độ phân phối Chi-bình phương với bậc tự do (100-1).

Bước 1: Lấy mẫu kích thước 100 từ phân phối chuẩn với trung bình 8 và độ lệch chuẩn là 2 sau đó tính phương sai ta được giá trị của biến ngẫu nhiên

> X=function(){
+ var(rnorm(100,8,2))
+ }
> X()
[1] 3.181167

Bước 2: Lặp lại quá trình trên 10000 lần để có mẫu

> MauX=replicate(10000,X())
> MauX
[1] 3.083733 3.931638 4.354841 2.926393 3.688206 4.631140 2.730177 4.428081
[9] 3.583060 3.519667 5.556578 4.034123 4.194960 4.559011 3.734663 3.863493

...

[9985] 4.477767 4.093669 3.949555 3.213602 4.653847 4.197430 4.356281 4.178395
[9993] 3.762838 3.627636 4.140599 4.323487 3.218310 4.046636 3.567655 3.601010

Bước 3: Thành lập mẫu cho biến ngẫu nhiên

> Y=(99*MauX)/4
> Y
[1] 76.32239 97.30804 107.78231 72.42822 91.28310 114.62071 67.57187
[8] 109.59501 88.68073 87.11177 137.52531 99.84454 103.82527 112.83551

...

[9990] 103.88639 107.81795 103.41528 93.13024 89.78399 102.47983 107.00629
[9997] 79.65318 100.15424 88.29947 89.12500

Bước 4: Vẽ đồ thị Histogram tần suất của mẫu trên với số khoảng 60 và so sánh với hàm mật độ của phân phối Chi-bình phương với 99 bậc tự do

> hist(Y,breaks=60,freq=FALSE)

> curve(dchisq(df=99,x),col="BLUE",add=TRUE)

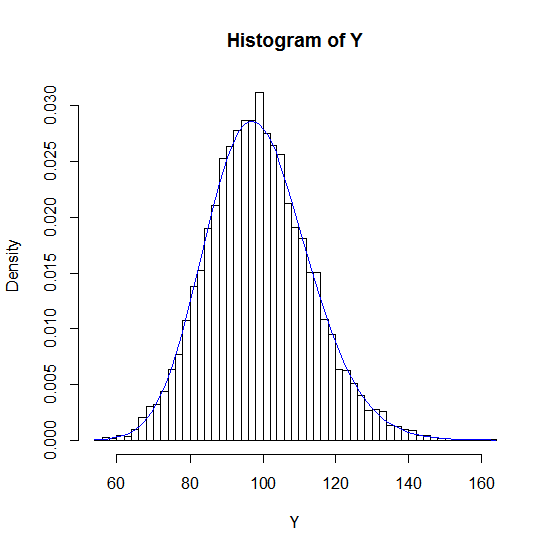
Phân phối mẫu cho tỷ lệ

Giả sử ta cần khảo sát đặc trưng A của tổng thể, khảo sát trên n phần tử và đặt

ta thu được mẫu ngẫu nhiên với , với p là tỉ lệ phần tử thỏa đặc trưng A.

Đặt là số phần tử thỏa đặc trưng A trong mẫu khảo sát, thì . Tỉ lệ mẫu được xác định bởi và . Theo định lý giới hạn trung tâm ta có sẽ hội tụ theo phân phối về phân phối chuẩn hóa